플로이드 와샬(Floyd Warshall) 알고리즘이란?
이전에 공부했던 다익스트라 알고리즘은 특정 정점에서 시작하여 다른 특정 정점 또는 모든 정점으로의 최단 경로를 구하는 알고리즘이었다. 플로이드 와샬 알고리즘 또한 다익스트라 알고리즘과 같이 최단 경로를 구하는 알고리즘이다.
다만 다익스트라 알고리즘과의 차이점은 "모든 정점에서 모든 정점으로의 최단 거리"를 구하는 알고리즘이라는 것이다.
또한 다익스트라 알고리즘에서는 가장 적은 비용을 하나씩 선택하며 알고리즘을 수행했지만, 플루이드 와샬 알고리즘은 거쳐가는 정점을 기준으로 알고리즘을 수행한다. 또한 다이나믹 프로그래밍 알고리즘에 의거한다.
동작 단계

위의 그래프를 예시로 들어보겠다.
이 때, 각 정점이 다른 정점으로 가는 비용을 배열의 형태로 보면 다음과 같다.
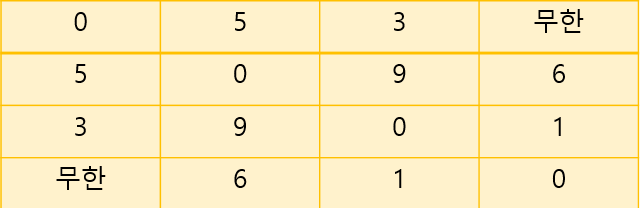
이 테이블(배열)은 곧 각 정점마다의 최소 비용이다.
이제 차례로 시작해보자.
위에서도 말했듯이 플로이드 와샬은 거쳐가는 정점을 기준으로 한다.
예시로 든 그래프는 4개의 노드가 있으므로 총 4번의 과정을 거쳐야 한다.
우선 1번 노드를 거친다고 하자.
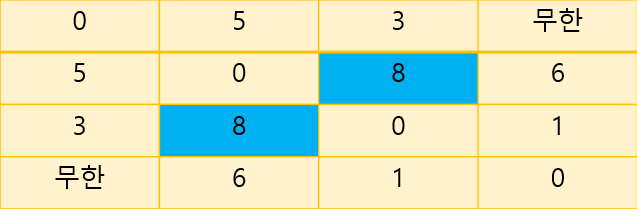
파란색으로 변한 부분을 보자. 2번 노드와 3번 노드를 왕복할 때 원래의 최소 비용은 9였으나, 1번 노드를 거치면서 8의 비용으로 갈 수 있게 되었다.
다음으로 2번 노드를 거쳐보자.
2번 노드를 통해 갈 수 있는 경우는 (1 - 2 - 3), (1 - 2 - 4) 총 2개의 왕복할 수 있는 길이 있다.
이 때 1 - 2 - 3은 2번 노드를 거친다면, 오히려 더 큰 비용이 들게 되므로 갱신하지 않는다.
하지만 1 - 2 - 4는 원래 서로 오갈수 없는 노드였지만, 2번 노드를 통해 거칠 수 있게 되었으므로 갱신해준다.
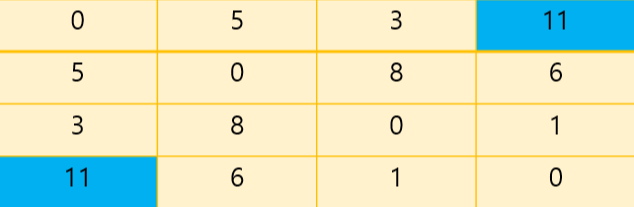
이번에는 3번 노드를 거쳐보자.
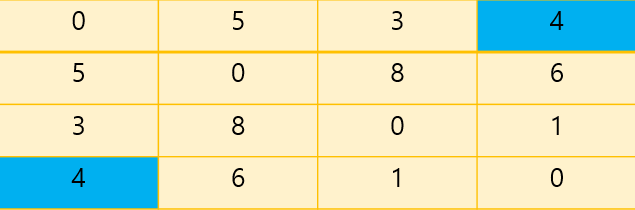
3번을 거치는 간선은 (1 - 3 - 2), (1 - 3 - 4), (2 - 3- 4)가 있다. 이 때, (1 - 3 - 2)와 (2 - 3 - 4)는 3번 노드를 거치게 되면 더 큰 비용이 필요하게 되므로 갱신하지 않는다. 하지만 1 - 3 - 4는 앞에서 2번 노드를 거쳐 가는 비용인 11보다 더 적은 비용으로 갈 수 있으므로 갱신을 해준다.
마지막으로 4번 노드를 거친다.
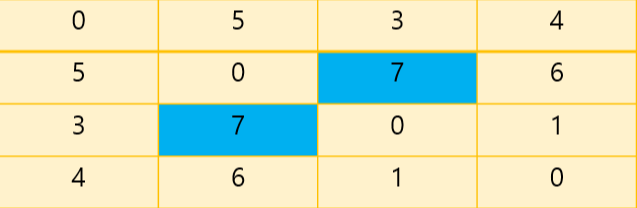
4번 노드를 거칠 수 있는 방법은 (2 - 4 - 3)이다. 앞에서 이미 2 - 3 노드 사이의 비용이 갱신되었었지만, 4번 노드를 거치므로서 더 적은 비용으로 이동할 수 있게 된다. 따라서 갱신해준다.
모든 노드를 거치는 과정이 끝났다.
이로써 갱신이 끝난 테이블이 각 정점 사이의 최소 비용이 되게 된다.
이를 코드로 구현해보자.
구현
private const val INF = 1000000
private const val num = 4
private val table = arrayOf(
intArrayOf(0, 5, 3, INF),
intArrayOf(5, 0, 9, 6),
intArrayOf(3, 9, 0, 1),
intArrayOf(INF, 6, 1, 0)
)
fun main() = with(System.`in`.bufferedReader()) {
floydWarshall()
}
fun floydWarshall() {
val cost = table
repeat(num) { node -> // 거쳐가는 노드
repeat(num) { startNode -> // 시작 노드
repeat(num) { endNode -> // 도착 노드
if(cost[startNode][node] + cost[node][endNode] < cost[startNode][endNode]) {
cost[startNode][endNode] = cost[startNode][node] + cost[node][endNode]
}
}
}
}
repeat(num) { i ->
repeat(num) { j ->
print("${cost[i][j]} ")
}
println()
}
}INF를 Int.MAX_VALUE로 잡게 된다면 오버 플로우가 발생하게 된다.
알고리즘을 사용할 때, 각각의 상황에 마다 INF 크기를 적절하게 정해줘야 한다.
'Algorithm' 카테고리의 다른 글
| [알고리즘] 위상 정렬(Topological Sort) (0) | 2022.09.10 |
|---|---|
| [알고리즘] 이분 그래프(Bipartite Graph) (0) | 2022.08.16 |
| [알고리즘] 다익스트라 알고리즘(Dijkstra Algorithm) (0) | 2022.08.03 |
| [알고리즘] 동적 프로그래밍(Dynamic Programming): 메모이제이션(Memoization), 테뷸레이션(Tabulation) (0) | 2022.07.26 |
| [알고리즘] 프림 알고리즘(Prim Algorithm) (0) | 2022.07.24 |


댓글