728x90
이분 그래프란?
정점을 두 그룹으로 나눌 수 있으면서, 같은 그룹끼리는 간선으로 이어지지 않은 그래프이다.
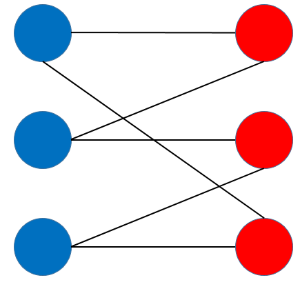
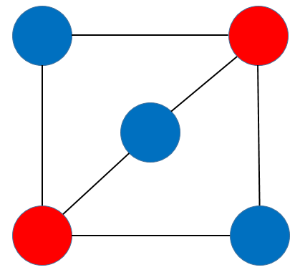
트리가 아닌 그래프이므로, 사이클이 있어도 상관없으나, 같은 색상의 정점끼리 연결은 있어서는 안된다.
간선이 단 한도 없고 정점만 있는 상태도 이분 그래프이다. 여기에서 알 수 있듯이, 모든 정점이 꼭 연결되있어야 하는 것이 아니다.
이분 그래프 구현
이분 그래프는 DFS 또는 BFS를 사용하여 구현할 수 있다.
나는 BFS가 더 익숙하여 BFS를 사용할 것이다.
백준의 1707번 이분 그래프 문제를 예시로 들어보자.
import java.util.*
import kotlin.collections.ArrayList
private lateinit var color: IntArray
private lateinit var graph: Array<ArrayList<Int>>
fun main() = with(System.`in`.bufferedReader()) {
val testCase = readLine().toInt()
repeat(testCase) {
val (nodeCnt, edgeCnt) = readLine().split(" ").map { it.toInt() }
graph = Array(nodeCnt + 1) { ArrayList() }
color = IntArray(nodeCnt + 1)
repeat(edgeCnt) {
val (from, to) = readLine().split(" ").map { it.toInt() }
graph[from].add(to)
graph[to].add(from)
}
if(bipartiteGraph(nodeCnt)) println("YES")
else println("NO")
}
}
private fun bipartiteGraph(n: Int): Boolean {
val que: Queue<Int> = LinkedList()
for(i in 1 ..n) {
if(color[i] == 0) {
que.add(i)
color[i] = 1
}
while(que.isNotEmpty()) {
val cur = que.poll()
val curColor = color[cur]
for(j in graph[cur].indices) {
val nextColor = color[graph[cur][j]]
if(nextColor == 0) que.add(graph[cur][j])
if(nextColor == color[cur]) return false
if(curColor == 1 && nextColor == 0) color[graph[cur][j]] = 2
else if(curColor == 2 && nextColor == 0) color[graph[cur][j]] = 1
}
}
}
return true
}
728x90
'Algorithm' 카테고리의 다른 글
| [알고리즘] 선택 정렬(Selection Sort) (1) | 2023.10.22 |
|---|---|
| [알고리즘] 위상 정렬(Topological Sort) (0) | 2022.09.10 |
| [알고리즘] 플로이드 와샬(Floyd Warshall) (0) | 2022.08.08 |
| [알고리즘] 다익스트라 알고리즘(Dijkstra Algorithm) (0) | 2022.08.03 |
| [알고리즘] 동적 프로그래밍(Dynamic Programming): 메모이제이션(Memoization), 테뷸레이션(Tabulation) (0) | 2022.07.26 |


댓글