위상 정렬(Topological Sort)
순서가 정해져 있는 작업을 어떠한 차례로 수행해야 하는지 결정해주는 알고리즘이다.
즉, 방향 그래프에 존재하는 정점들의 선행 순서를 위반하지 않고 모든 정점을 나열하는 것이다.

위상 정렬은 한 방향 그래프에서 여러 위상 정렬이 가능하다.
즉, 답이 여러가지일 수 있다는 것이다.
위 방향그래프에서 위상 정렬을 한 결과를 생각해보면 다음과 같다.
- 1 → 6 → 2 → 5 → 4 → 3
- 6 → 2 → 1 → 5 → 4 → 3
- 6 → 1 → 2 → 5 → 4 → 3
과정
- 진입 차수가 0인 정점을 큐에 저장한다.
- 큐에서 원소를 꺼내 연결된 모든 간선을 제거한다.
- 간선 제거 이후 진입 차수가 0인 정점을 큐에 저장한다.
- 큐가 빌 때까지 반복한다. 이때, 모든 원소를 방문하기 전 큐가 빈다면 사이클이 존재하는 것이므로 위상 정렬을 할 수 없다는 것을 의미한다.
위에서 예시로 들었던 사진을 다시 한번 보자.

진입 차수가 0인 정점은 1과 6이 있다.
이 중 아무거나 먼저 큐에 저장하면 되는데, 나는 1부터 큐에 저장해보겠다.
큐에 저장 후, 이를 큐에서 꺼내 정렬 순서를 저장할 배열에 저장해주며, 연결된 간선들을 모두 제거해준다.
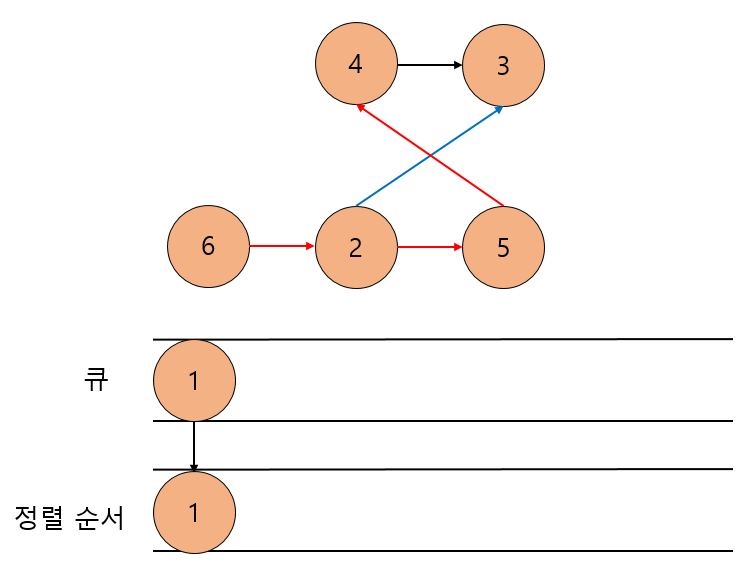
다음으로 진입 차수가 0인 정점은 6이 있다.
4는 5에서 오는 경로가 있으므로 진입 차수가 0이 아니다.
위의 과정을 그대로 정점 6 또한 큐에 저장 후, pop 하여 정렬 순서를 저장할 배열에 저장한 후, 이와 연결된 모든 간선을 제거해준다.

다음으로 진입 차수가 0인 정점은 2이다.
즉, 2를 위에서 했던 과정을 반복해준다.

이제 그림이 필요가 없을 것 같아 설명으로만 하겠다.
남은 5, 4, 3 정점에서 진입 차수가 0인 것은 5이다.
따라서 5가 다음 순서가 되고, 그 이후로 4, 3이 차례로 들어가게 된다는 것을 알 수 있다.
결론적으로, 1 → 6 → 2 → 5 → 4 → 3이라는 순서를 얻을 수 있다.
만약 처음에 6부터 저장했다면 6 → 2 → 1 → 5 → 4 → 3이 될 수도 있고,
6 → 1 → 2 → 5 → 4 → 3이 될 수도 있다.
구현
import java.util.*
import kotlin.collections.ArrayList
private val graph = ArrayList<ArrayList<Int>>()
private val degree = IntArray(7)
fun main() {
for(i in 0 .. 6) graph.add(ArrayList())
graph[1].add(4)
degree[4]++
graph[4].add(3)
degree[3]++
graph[6].add(2)
degree[2]++
graph[2].add(5)
degree[5]++
graph[5].add(4)
degree[4]++
graph[2].add(3)
degree[3]++
topologicalSort()
}
private fun topologicalSort() {
val sb = StringBuilder()
val que: Queue<Int> = LinkedList()
val result = ArrayList<Int>()
for(i in 1 .. 6) {
if(degree[i] == 0) que.add(i)
}
while(que.isNotEmpty()) {
val cur = que.poll()
result.add(cur)
for(next in graph[cur]) {
degree[next]--
if(degree[next] == 0) que.add(next)
}
}
if(result.size != 6) println("위상 정렬을 완료할 수 없습니다.")
for(i in result) sb.append("$i ")
println(sb.toString())
}'Algorithm' 카테고리의 다른 글
| [알고리즘] 버블 정렬(Bubble Sort) (0) | 2023.10.22 |
|---|---|
| [알고리즘] 선택 정렬(Selection Sort) (1) | 2023.10.22 |
| [알고리즘] 이분 그래프(Bipartite Graph) (0) | 2022.08.16 |
| [알고리즘] 플로이드 와샬(Floyd Warshall) (0) | 2022.08.08 |
| [알고리즘] 다익스트라 알고리즘(Dijkstra Algorithm) (0) | 2022.08.03 |


댓글