프림 알고리즘
무방향 연결 그래프가 주어졌을 때, 최소 신장 트리를 찾기 위한 알고리즘이다.
크루스칼 알고리즘과의 목적은 같지만, 언제 어떻게 사용하느냐에 따라 효율성이 달라질 수 있다.
크루스칼 알고리즘에 관해서는 크루스칼 알고리즘을 참고하면 된다.
크루스칼 알고리즘과 마찬가지로 프림 알고리즘도 그리디 알고리즘(Greedy Algorithm)의 일종이다.
크루스칼 알고리즘은 간선의 가중치를 오름차순으로 정렬해서 가장 작은 가중치를 가진 간선부터 선택해나갔다.
프림 알고리즘은 임의의 시작 정점에서 정점을 추가해가며 단계적으로 트리를 확장시키는 기법이다.
프림 알고리즘의 동작
위에서도 말했듯이, 프림 알고리즘은 그리디 알고리즘의 일종이다.'
즉, 탐색 정점과 연결된 인접 정접들 중 가중치가 가장 적은 간선으로 연결된 정점을 선택한다.
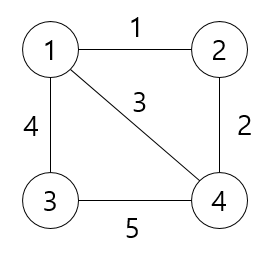
나는 1번 노드를 정점으로 잡을 것이다.
1번 노드에서 인접한 정점은 2, 3번 노드가 있다.
이 때, 2번 노드와 연결된 간선의 값이 가장 작으므로 2번 노드를 선택한다.
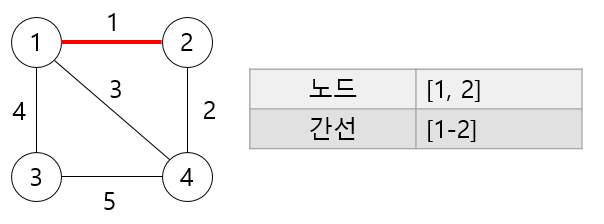
1,2 노드와 인접한 노드로는 3번 노드, 4번 노드가 있다.
1-3 간선보다 2-4 간선의 가중치가 더 작으므로 4번 노드를 선택한다.

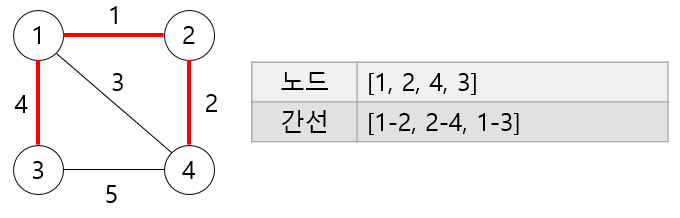
이제 1, 2, 4 노드와 인접한 노드들을 보자.
이미 선택된 노드는 선택될 일이 없기 때문에 1-4 간선은 고려를 하지 않아도 된다.
그렇다면 남은 간선은 1-3 간선과 4-3 간선이 있다.
이 때 1-3 간선의 가중치가 더 적으므로 1-3 간선이 선택된다.
프림 알고리즘 구현
백준의 1197번인 최소 스패닝 트리를 프림 알고리즘을 이용해 구현해 보도록 하자.
https://www.acmicpc.net/problem/1197
1197번: 최소 스패닝 트리
첫째 줄에 정점의 개수 V(1 ≤ V ≤ 10,000)와 간선의 개수 E(1 ≤ E ≤ 100,000)가 주어진다. 다음 E개의 줄에는 각 간선에 대한 정보를 나타내는 세 정수 A, B, C가 주어진다. 이는 A번 정점과 B번 정점이
www.acmicpc.net
import java.util.PriorityQueue
private lateinit var edge: Array<ArrayList<Pair<Int, Int>>>
private lateinit var visited: BooleanArray
data class Info(val cost: Int, val node: Int): Comparable<Info> {
override fun compareTo(other: Info): Int = cost - other.cost
}
fun main() = with(System.`in`.bufferedReader()){
val (nodeCnt, edgeCnt) = readLine().split(" ").map { it.toInt() }
edge = Array(nodeCnt + 1) { ArrayList() }
visited = BooleanArray(nodeCnt + 1)
repeat(edgeCnt) {
val (start, end, cost) = readLine().split(" ").map { it.toInt() }
edge[start].add(Pair(cost, end))
edge[end].add(Pair(cost, start))
}
println(prim())
}
private fun prim(): Long {
var ans = 0L
val pq = PriorityQueue<Info>()
pq.add(Info(0, 1))
while(pq.isNotEmpty()) {
val cur = pq.poll()
if(visited[cur.node]) continue
visited[cur.node] = true
ans += cur.cost
for(i in 0 until edge[cur.node].size) {
if(!visited[edge[cur.node][i].second]) {
pq.add(Info(edge[cur.node][i].first, edge[cur.node][i].second))
}
}
}
return ans
}'Algorithm' 카테고리의 다른 글
| [알고리즘] 다익스트라 알고리즘(Dijkstra Algorithm) (0) | 2022.08.03 |
|---|---|
| [알고리즘] 동적 프로그래밍(Dynamic Programming): 메모이제이션(Memoization), 테뷸레이션(Tabulation) (0) | 2022.07.26 |
| [알고리즘] 크루스칼 알고리즘(Kruscal Algorithm) (0) | 2022.07.21 |
| [알고리즘] 최소 신장 트리(MST, Minimum Spanning Tree) (0) | 2022.07.21 |
| [알고리즘] 그래프 탐색(Graph Search) /BFS, DFS (1) | 2022.06.02 |


댓글