그래프
- 그래프란 공집합이 아닌 노드(vertex, node)들의 유한 집합 V와 이 노드들을 연결하는 간선(edge)들의 집합 E로 구성된다.
-> G = (V, E), |V| = n, |E| = m - 트리는 그래프의 한 종류이다. 그래프에서 사이클이 존재하지 않으면 곧 트리이다.
- 노드의 차수: 노드에 연결된 간선의 수를 말하며, 방향 그래프에서는 진입 차수(indegree)와 진출 차수(outdegree)로 나누어 고려한다.
- 경로(path): 두 개의 노드를 연결하는 일련의 노드들
- 노드 a에서 b까지의 경로 a, v1, v2, . . . , vk, b가 존재하기 위해서는
간선 (a, v1), (v1, v2), . . ., (vn-1, vk), (vk, b)가 존재해야 한다.
- 단순 경로: 한 노드를 두 번 거치지 않는 경로 - 경로의 길이
- 가중치 그래프: 경로를 구성하는 간선의 가중치 합
- 비가중치 그래프: 경로를 구성하는 간선의 수 - 주기(cycle): 첫 번째 노드와 마지막 노드가 같은 경로
- 그래프의 간선 수가 최대 간선 수에 가까우면 밀집(densse) 그래프
- 반대로 간선 수가 0에 가까우면 희소(sparse) 그래프라 한다.
n개의 노드로 구성된 무방향 그래프의 최대 간선 수
1. 진출과 진입이 같은 간선의 존재 고려: n(n+1) / 2 = n(n-1) / 2 + n
2. 진출과 진입이 같은 간선을 고려하지 않으면: n(n-1) / 2
- 연결 무방향 그래프의 최소 간선 수: n - 1(트리의 간선 수)
그래프의 종류
1. 연결 그래프(connected graph)
- 그래프에서 서로 다른 모든 노드 쌍 사이에 경로가 존재하는 그래프
2. 완전 그래프(complete graph)
- 모든 노드가 인접 노드가 되는 그래프
- 완전 그래프이면 연결 그래프이지만 반대는 성립하지 않는다.
3. 부분 그래프(subgraph)
- V' ⊂ V, E' ⊆ E가 성립하면 G' = (V', E')는 G = (V, E)의 부분 그래프라 한다.
4. 유한 그래프: 노드의 수가 유한한 그래프
- 반대 개념: 무한 그래프
5. 무방향 그래프(undirected graph): 간선의 방향성이 없는 그래프
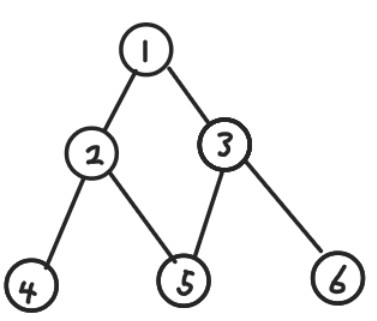
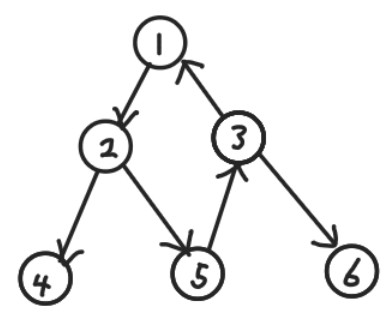
6. 방향 그래프(directed graph, digraph): 간선의 방향성이 있는 그래프
- 방향 그래프에서 간선을 아크(arc)라고도 한다.
7. 가중치 그래프(weighted graph): 간선에 가중치가 있는 그래프
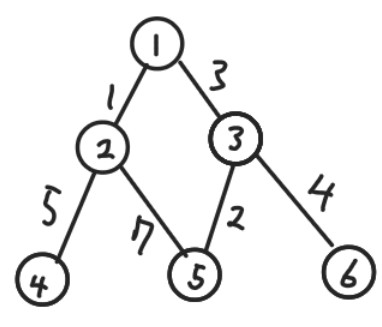
8. 비가중치 그래프: 간선에 가중치가 없는 그래프
- 방향성이 있다면 방향 그래프와 같고, 없다면 무방향 그래프와 같다.
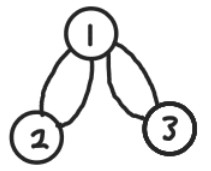
9. 다중 그래프(multigraph): 두 노드를 잇는 간선이 여러 개 존재할 수 있다.
- 이와 같은 간선을 병행 간선(parallel edge)이라 한다.
그래프를 자료구조로 표현하는 방법
1. 인접 행렬
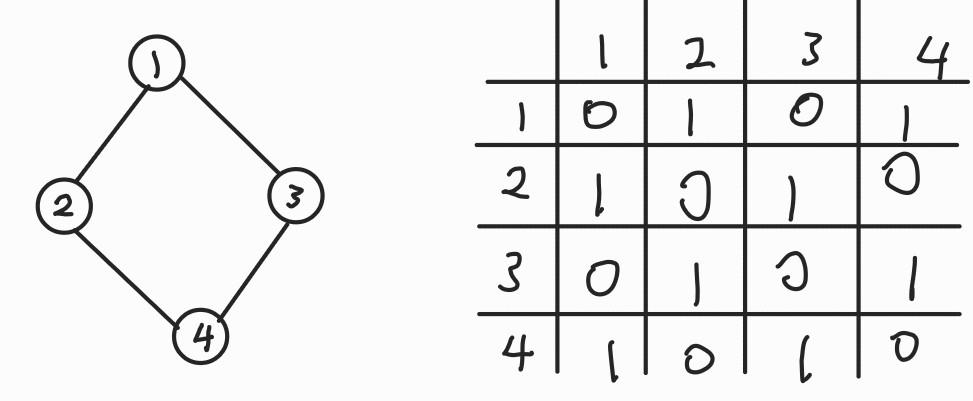
장점:
- 밀집 방향 그래프에 유리한 방식이다.
단점:
- n2 공간이 필요하다.
- 가중치 그래프에서 가중치 값의 범위에 따라 간선이 없는 경우를 표현하기 힘들 수 있다.
2. 인접 리스트
- 실제 구현에서는 연결 리스트를 꼭 사용하지 않고, 배열 리스트를 사용하는 경우도 많다.
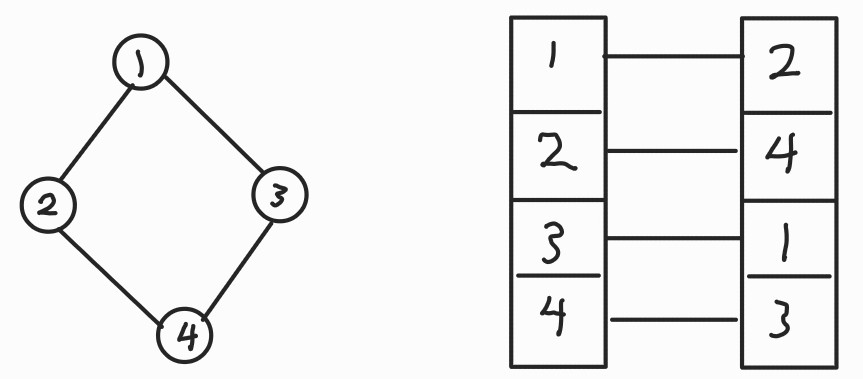
장점:
- 희소 무방향 그래프에 유리하다.
단점:
- 방향 그래프에서는 진입 차수를 계산하는 것이 힘들다.
- 역인접 리스트 유지 -> 차라리 인접 행렬이 낫다.
일반 그래프 탐색

선택 기준 측면에서 생각을 해보면
- 출발 노드가 있으므로 첫 번째 선택 가능한 간선은 출발 노드에서 진출하는 간선 중 하나이다.
- 특정 노드를 선택하였다면 그다음 반복에서는 두 노드에서 진출하는 간선 중에서 선택해야 한다.
목표를 생각하면
- 출발 노드로부터 도달 가능한 모든 노드를 찾는 것이 목표이다.
- 출발 노드에서 진출 간선에 의해 연결된 모든 노드는 최종 답에 포함되어야 한다.
- 이 노드의 진출 간선에 의해 연결된 모든 노드도 최종 답에 포함되어야 한다.
- 이 과정을 반복하면 목표에 달성할 수 있다.
- 출발 노드에서 진출 간선에 의해 연결된 모든 노드를 저장하여 처리
→ 저장 위치는 리스트, 큐, 스택, 우선순위 큐 등 다양하다.
- 먼저 꼭 처리해야 하는 노드는 없고, 처리한 노드는 다시 고려할 필요가 없다.
→ 처리한 순서대로 자료구조에서 제거해야 한다.
일반 그래프 탐색의 정확성 증명
출발 노드가 s일 때, 알고리즘이 종료되어 v가 답에 포함되기 위한 필요충분조건으로 s에서 v까지의 경로가 있어야 한다.
- v가 포함되면 s에서 v까지 경로가 있다.
- s에서 v까지 경로가 있으면 v는 최종적으로 포함된다.
BFS vs DFS
1. BFS
- 큐를 사용하여 구현한다.
- 선택된 노드와 인접한 모든 노드를 먼저 방문한다.
- 무방향 비가중치 그래프에서 최단 경로를 구할 수 있다.
- 무방향 그래프에서 연결 여부 확인에 사용한다. (방향도 가능하다.)
2. DFS
- 스택을 사용하여 구현(재귀적으로도 구현 가능하다.)
- 선택된 노드의 첫 번째 인접 노드를 방문하고, 그 노드의 첫 번째 인접 노드를 방문하는 형태이다.
- 방향 그래프에서 연결 여부 확인에 사용한다. (무방향도 가능하다.)
보통 무방향 그래프 문제는 BFS, 방향 그래프 문제는 DFS를 사용한다.
하지만 그래프의 모습과 해결하고자 하는 문제의 특성에 의해 탐색 방법을 결정해야 한다.
BFS를 이용한 그래프 탐색
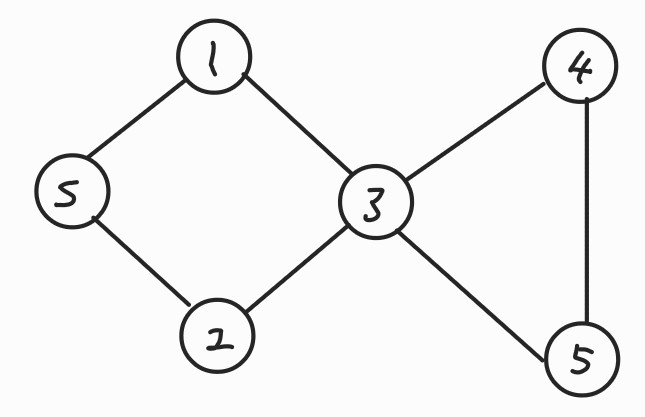
같은 거리에 있는 노드들 순으로 방문한다.
- while 루프 이전: O(n)
- 큐 생성, visited 배열 초기화 등 기본적인 입출력을 한다. - 바깥 while 루프: n번 반복
- 한 번에 하나의 노드 처리 - 내부 for루프
- 인접 행렬: n번 반복 -> O(n2)
- 인접 리스트: 각 노드의 간선 수에 좌우
- 전체적으로 모든 간선을 고려한다 -> O(m) - 큐 연산: O(n)
- 전체 비용
- 인접 행렬: O(n2 + m) = O(n2)
- 인접 리스트: O(m + n) - 무방향, 방향 차이가 없다.

s = starting node
Q = empty queue of nodes
visited[s] = true
Q.enqueue(s)
while Q is not empty do
v = Q.dequeue()
for each edge (v, w) do
if not visited[w] then
visited[w] = true
Q.enqueue(w)BFS를 이용한 최단 경로
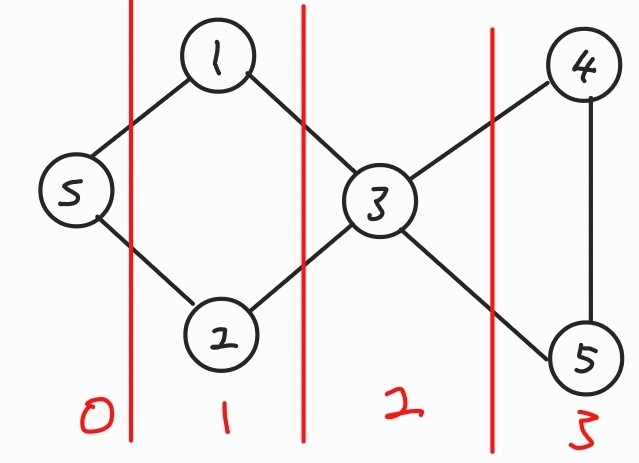
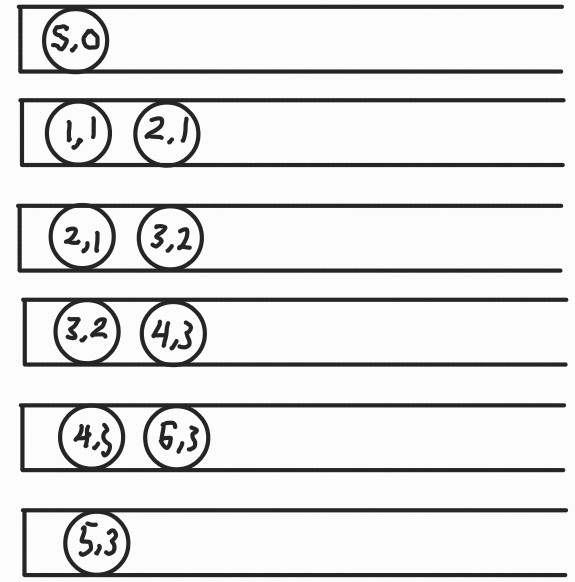
s = starting node
visited[s] = true
distanceps[ - 0 and distance[x] = INF for rest
Q = queue of nodes with distances
Q.enqueue(s)
while Q is not empty do
v = Q.dequeue()
for each edge (v, w) do
if not visited[w] then
visited[w] = true
distance[w] = distance[v] + 1
Q.enqueue(w)- visited를 사용하지 않고 distance만 이용이 가능하다.
- 경로 자체
1) distance를 이용하여 거꾸로 계산
2) 진행하면서 이전 노드 정보 기록 prevNode[w] = v
BFS를 이용한 연결 여부 확인
- 모든 연결 component(부분 그래프)를 구하는 알고리즘
components = []
set visited[] to all false
for i=1 to n do
if visited[i] then
// i를 출발 노드로 방문 가능한 모든 노드를 리스트로 구축하여 반환하도록 BFS 수정
components.add(BFS(G, i));
DFS를 이용한 그래프 탐색
- 계속 아래로 탐색을 진행한다.
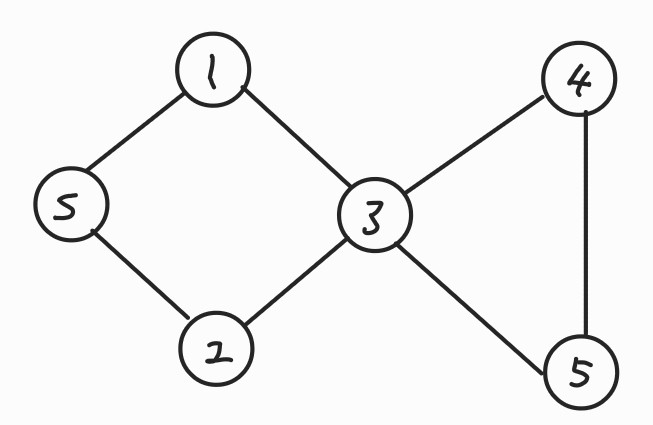
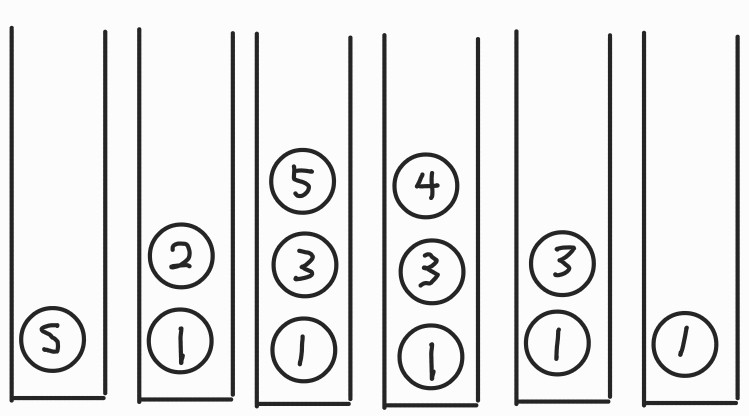
s = starting node
S = empty stack of nodes
visited[s] = true
S.push(s)
while S is not empty do
v = S.pop()
for each edge (v, w) do
if not visited[w] do
visited[w] = true
S.push(w)
DFS(G, s) {
visited[s] = true
for each edge (s, w) do
if not visited[w] then
DFS(G, w)
}- 재귀 버전 vs 비재귀 버전, |V| = n
- 재귀 버전은 재귀 호출 깊이에 의존
- 최악의 경우: 출발 노드부터 모든 노드가 선형적으로 연결되어 있다면 호출 깊이가 n에 비례한다.
- 비재귀 버전은 스택 공간에 의존
- 최악의 경우: 다른 모든 노드가 출발 노드의 이웃 노드이면 첫 반복에서 n-1개 노드가 스택에 push된다.
- 실제 사용된 공간은 스택 구현 방법에 따라 차이가 있을 수 있다.
- 최악의 경우: 다른 모든 노드가 출발 노드의 이웃 노드이면 첫 반복에서 n-1개 노드가 스택에 push된다.
- 재귀 버전은 재귀 호출 깊이에 의존
'Algorithm' 카테고리의 다른 글
| [알고리즘] 크루스칼 알고리즘(Kruscal Algorithm) (0) | 2022.07.21 |
|---|---|
| [알고리즘] 최소 신장 트리(MST, Minimum Spanning Tree) (0) | 2022.07.21 |
| [알고리즘] 퀵 정렬(Quick Sort) - 랜덤 피벗 (0) | 2022.04.14 |
| [알고리즘] 퀵 정렬(Quick Sort) - 피벗을 맨 끝 값으로 잡았을 때 (0) | 2022.04.13 |
| [알고리즘] 퀵 정렬(Quick Sort) - pivot(피벗)을 첫 값으로 잡았을 때 (0) | 2022.04.13 |


댓글