728x90
신장 트리(Spanning Tree)
신장 트리는 연결 그래프의 부분 그래프이다.
그래프의 모든 정점과 간선의 부분 집합으로 구성되는 트리이고, 모든 노드는 적어도 하나의 간선에 연결이 되어있어야 한다.
또한 이름에서 알 수 있듯이, 트리이므로 사이클이 존재해서는 안된다.
연결 그래프이므로, DFS(깊이 우선 탐색), BFS(너비 우선 탐색)를 이용하여 구현이 가능하다.
이 때 연결 그래프에는 하나의 신장트리 뿐만이 아닌 다양하게 존재할 수 있다.
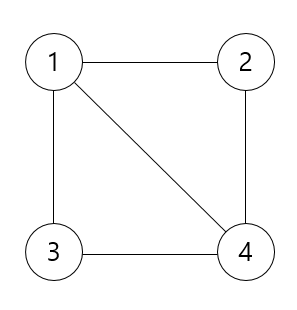
이와 같은 연결 그래프가 있을 때, 나올 수 있는 신장 트리는 다음과 같다.
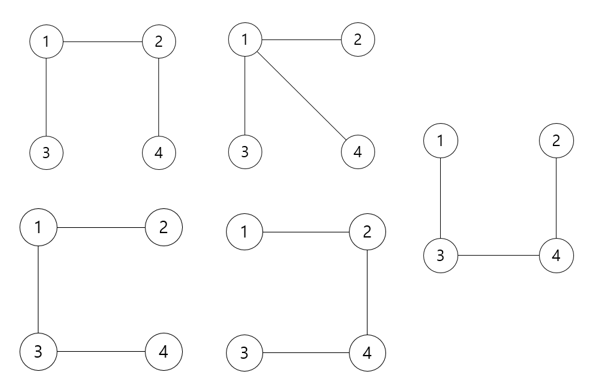
최소 신장 트리(Minimum Spanning Tree)
위에서 신장 트리에 대해 알아보았다.
그래프의 간선에 가중치가 있다면, 그것을 가중치 그래프라고 한다.
가중치 무방향 그래프에서의 신장 트리의 비용은 신장 트리를 구성하는 간선들의 가중치 합이다.
즉, 최소 신장 트리는 비용이 최소가 되는 신장트리를 뜻한다.
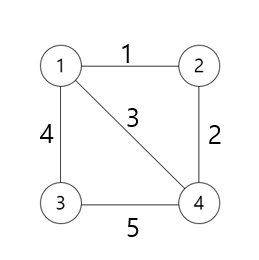
위의 가중치 무방향 그래프에서의 최소 신장 트리는 다음과 같다.
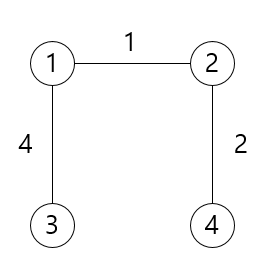
이러한 최소 신장 트리를 구하는 대표적인 알고리즘에는
크루스칼 알고리즘(Kruskal Algorithm)과 프림 알고리즘(Prim Algorithm)이 있다.
이는 이후에 정리할 것이다.
728x90
'Algorithm' 카테고리의 다른 글
| [알고리즘] 프림 알고리즘(Prim Algorithm) (0) | 2022.07.24 |
|---|---|
| [알고리즘] 크루스칼 알고리즘(Kruscal Algorithm) (0) | 2022.07.21 |
| [알고리즘] 그래프 탐색(Graph Search) /BFS, DFS (1) | 2022.06.02 |
| [알고리즘] 퀵 정렬(Quick Sort) - 랜덤 피벗 (0) | 2022.04.14 |
| [알고리즘] 퀵 정렬(Quick Sort) - 피벗을 맨 끝 값으로 잡았을 때 (0) | 2022.04.13 |


댓글