문제
https://www.acmicpc.net/problem/1647
1647번: 도시 분할 계획
첫째 줄에 집의 개수 N, 길의 개수 M이 주어진다. N은 2이상 100,000이하인 정수이고, M은 1이상 1,000,000이하인 정수이다. 그 다음 줄부터 M줄에 걸쳐 길의 정보가 A B C 세 개의 정수로 주어지는데 A번
www.acmicpc.net
해설
1. 마을의 이장은 마을을 두 개의 분리된 마을로 분할할 계획을 가지고 있다.
2. 마을에는 집이 하나 이상 있어야 한다.
3. 각 분리된 마을 안에서도 임의의 두 집 사이에 경로가 항상 존재하게 하면서 길을 더 없앨 수 있다.
4. 마을의 이장은 위 조건을 만족하도록 길들을 모두 없애고 나머지 길의 유지비의 합을 최소로 하고 싶다.
위는 문제에서 핵심이 되는 조건이라 생각된다.
각 마을에서 모든 집을 연결하면서 최소 비용을 구하는 문제이므로 최소 신장 트리를 사용하면 된다.
크루스칼 알고리즘과 프림 알고리즘 중 선택해서 해결하면 된다.
두 개의 마을로 나눌 때, 어떻게 해야 비용이 최소가 될까?

이 때, 최대 비용을 가진 간선을 나누면 된다.
최대 간선이 빠졌으므로 분리된 마을은 당연히 최소 비용으로 집들이 연결되 있게 된다.
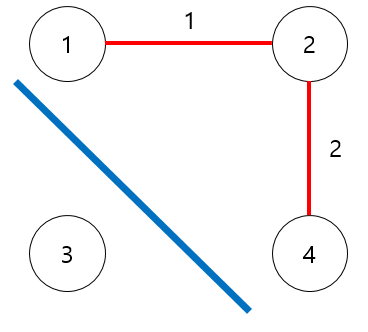
결론적으로 구현을 할 때, 원래라면 (노드의 갯수 - 1)이 될 때까지 크루스칼 알고리즘 또는 프림 알고리즘을 실행했다면,
이 문제에서는 (노드의 갯수 - 2)일 때까지 실행을 시켜주면 되는 문제이다.
소스 코드
import java.util.*
private lateinit var parent: IntArray
private val pq = PriorityQueue<Info>()
private var homeCnt = 0
private var roadCnt = 0
data class Info(val start: Int, val end: Int, val cost: Int): Comparable<Info> {
override fun compareTo(other: Info): Int = cost - other.cost
}
fun main() = with(System.`in`.bufferedReader()) {
val st = StringTokenizer(readLine())
homeCnt = st.nextToken().toInt()
roadCnt = st.nextToken().toInt()
parent = IntArray(homeCnt + 1)
repeat(homeCnt + 1) { i -> parent[i] = i}
repeat(roadCnt) { i ->
val (start, end, cost) = readLine().split(" ").map { it.toInt() }
pq.add(Info(start, end, cost))
}
println(kruskal())
}
private fun kruskal(): Int {
var ans = 0
var count = 0
while(count != homeCnt - 2) {
val cur = pq.poll()
if(find(cur.start) != find(cur.end)) {
union(cur.start, cur.end)
ans += cur.cost
count++
}
}
return ans
}
private fun union(a: Int, b: Int) {
val aParent = find(a)
val bParent = find(b)
parent[bParent] = aParent
}
private fun find(node: Int): Int {
if(parent[node] != node) parent[node] = find(parent[node])
return parent[node]
}'PS(Problem Solving) > BOJ' 카테고리의 다른 글
| [백준/BOJ] 21924번: 도시 건설 (1) | 2022.07.27 |
|---|---|
| [백준/BOJ] 4386번: 별자리 만들기 (0) | 2022.07.27 |
| [백준/BOJ] 13418번: 학교 탐방하기 (0) | 2022.07.26 |
| [백준/BOJ] 14621번: 나만 안되는 연애 (0) | 2022.07.25 |
| [백준/BOJ] 16398번: 행성 연결 (0) | 2022.07.24 |


댓글