도사정리
재귀 관계씩으로 표현한 알고리즘의 동작 시간을 점근적으로 계산하여 간단하게 계산하는 방법으로, 재귀 알고리즘의 시간 복잡도를 결정해주는 블랙박스 툴이다.
재귀 알고리즘의 점화식(recurrence)으로부터 시간 복잡도를 결정하며, 표준 점화식으로만 가능하다.
f(n)이 점근적으로 양이라는 말은 충분히 큰 n에 대해 f(n)이 양이라는 의미이다.
표준 점화식
3개의 파라미터로 구성된 대부분 재귀 알고리즘을 분석할 때 사용할 수 있는 점화식을 표준 점화식이라 한다.
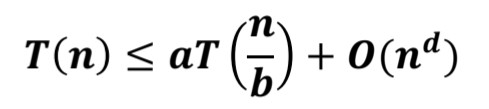
여기서 a는 재귀호출의 수, b는 입력 크기가 줄어드는 정도, d는 일반 과정에서 소요되는 시간 복잡도의 지수이다.
(a는 작을수록 좋으며, b는 클수록 좋다.)
a, b, d는 모두 n과 독립적인 상수이고, d=0이라면 상수 시간을 뜻한다.
※ 재귀 호출의 입력 크기는 항상 같은 수준으로 줄여야 한다.
표준 점화식으로 표현할 수 있는 재귀 알고리즘의 시간 복잡도는 다음과 같다.
Case1. a = bd, T(n) = O(ndlogn) -> 로그의 기저를 무시 가능하다.
Case2. a < bd, T(n) = O(nd)
Case3. a > bd, T(n) = O(nlogba) -> 로그의 기저를 무시 불가능하다.
Case1에서 log의 base는 중요하지 않지만 Case3에서는 중요하다.
-> Case1에선 base가 바뀌더라도 그 차이가 일정한 상수만큼의 차이만 발생하며, 이는 빅O에 의해 무시된다.
ex 1) T(n) <= 4T(n/2) + O(n)
-> a = 4, b = 2, d = 1
bd = 2 < a
∴ T(n) = O(nlog24) = O(n2)
ex 2) T(n) = 3T(n/2) + O(n)
-> a = 3, b = 2, d = 1
bd = 2 < a
∴ T(n) = O(nlog23) = O(n1.59)
식의 해석
a: RSP(rate of subproblem proliferation, 소문제 수 증가률) - evil, 커질수록 성능이 낮아진다.
bd: RWS(rate of work shrinkage, 문제 크기 축소률) - good, 커질수록 성능이 높아진다.
- RSP = RWS: 모든 레벨에서 해야 할 일이 같다.
- 도사정리 Case1 예) 합병정렬 - RSP < RWS: 레벨이 증가할수록 해야 할 일은 줄어든다.
- 도사정리 Case2
- 대부분의 일이 루트 레벨에서 이루어진다. - RSP > RWS: 레벨이 증가할수록 해야 할 일이 증가한다.
- 도사정리 Case3
- 대부분의 일이 단말 레벨에서 이루어진다.
'Algorithm' 카테고리의 다른 글
| [알고리즘] 퀵 정렬(Quick Sort) - pivot(피벗)을 첫 값으로 잡았을 때 (0) | 2022.04.13 |
|---|---|
| [알고리즘] 퀵 정렬(Quick Sort) - pivot(피벗)을 중앙으로 잡았을 때 (2) | 2022.04.10 |
| [알고리즘] 분할 정복(Divide & Conquer) (0) | 2022.04.06 |
| [알고리즘] 재귀 함수, 꼬리 재귀 (0) | 2022.04.06 |
| [알고리즘] Brute Force Algorithm(전수 조사 알고리즘) (0) | 2022.04.04 |


댓글