728x90
분할정복이란?
문제를 나눌 수 없을 때까지 나누어 각 작은 사례에 대한 해답을 얻고, 이들을 결합하여 원 문제에 대한 해답을 얻는
알고리즘이다.
시간복잡도는 O(nlogn)이며, 공간복잡도는 O(n)을 갖는다.
보통 다차시간 알고리즘의 성능을 개선하기 위해 사용한다.
분할정복의 전략
- 문제를 같은 유형의 작은 문제로 나눈다. (Divide)
- 작은 문제를 재귀적으로 해결한다.
- 해결 결과를 결합하여 원래의 문제에 대한 해결책을 제시한다. (Conquer)
합병 정렬(Merge Sort)
일반적인 방법으로 구현했을 때, 안정 정렬에 속한다.
구체적인 방법을 알아보면, 하나의 리스트를 두 개의 균등한 크기로 분할, 정렬한 후, 정렬된 두 리스트를 합하여 하나의 정렬된 리스트가 되게 하는 것이다.
합병 정렬의 단계는 다음과 같다.
- 분할(Divide): 배열을 2개의 부분 배열로 나눈다.
- 정복(Conquer): 부분 배열을 정렬한다. 부분 배열의 크기가 충분히 작지 않다면, 순환 호출을 통해 다시 분할을 시킨다.
- 결합(Combine): 정렬된 배열을 결합시킨다.
합병 정렬에는 추가적인 리스트가 필요하며, 각 부분 배열을 정렬할 때도 합병 정렬을 순환적으로 호출하여 적용한다.
합병 정렬에서 실제 정렬이 이루어지는 시점은 2개의 리스트를 합병하는 단계이다.
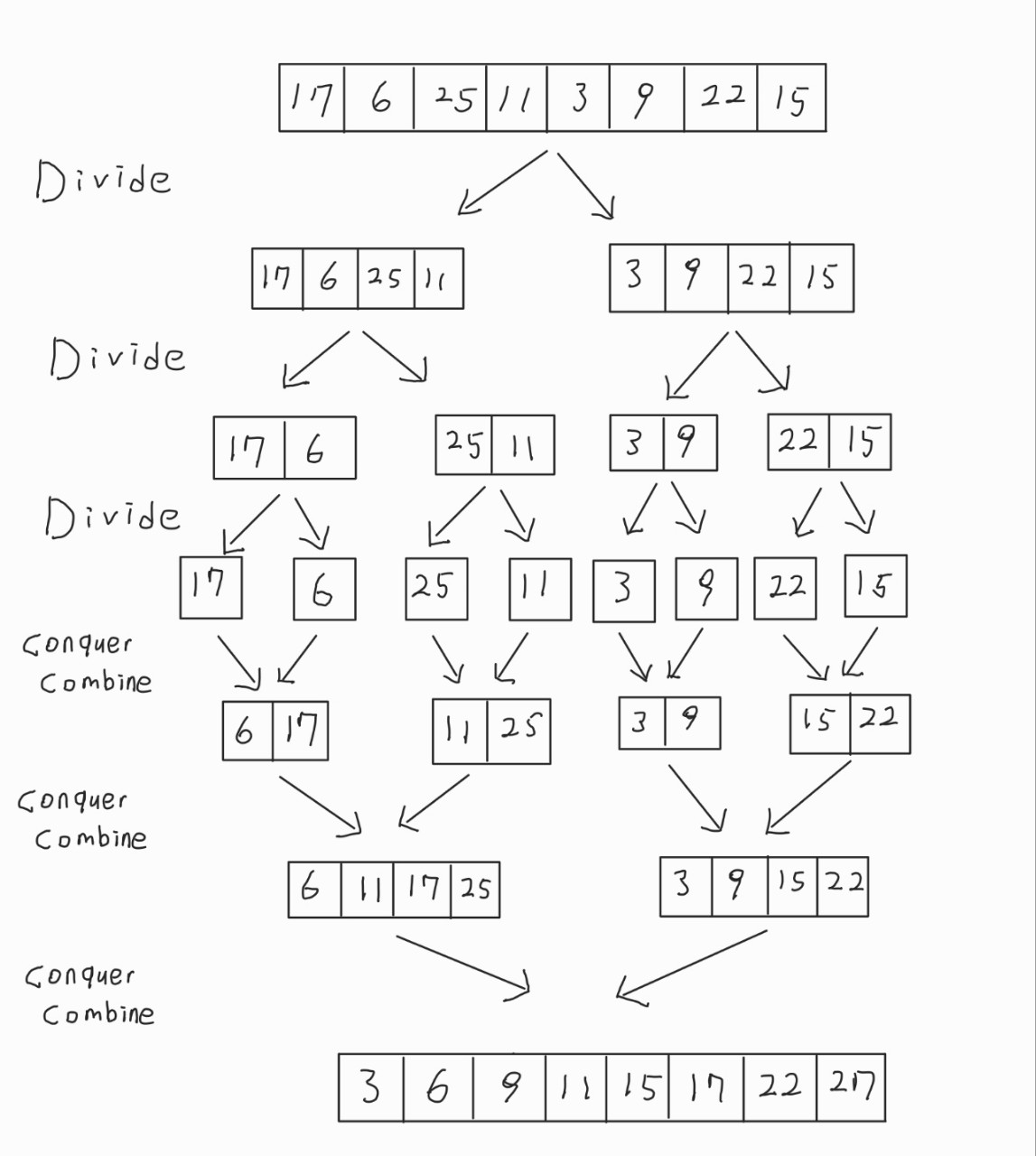
합병 정렬 예제
위의 그림과 같이 {17, 6, 25, 11, 3, 9, 22, 15} 배열이 있다고 하자.
이를 오름차순으로 정렬시키는 코드를 짜볼 것이다.
public class mergeSort {
public static void main(String[] args) {
int[] arr = {17, 6, 25, 11, 3, 9, 22, 15};
int[] sorted = new int[arr.length];
divide(arr, sorted,0, arr.length-1);
for(int i=0; i<arr.length; i++) System.out.print(arr[i] + " ");
System.out.println();
}
public static void divide(int[] arr, int[] sorted, int left, int right) { // 분할 단계
if(left < right) {
int mid = (left + right) / 2; // mid를 기준으로 부분 배열을 만든다.
divide(arr, sorted, left, mid);
divide(arr, sorted,mid+1, right);
conquer(arr, sorted, left, right);
}
}
public static void conquer(int[] arr, int[] sorted, int left, int right) { // 결합 단계
int mid = (left + right) / 2;
int leftIdx = left;
int rightIdx = mid + 1;
int saveIdx = left;
while(leftIdx <= mid && rightIdx <=right) {
if(arr[leftIdx] < arr[rightIdx]) sorted[saveIdx++] = arr[leftIdx++];
else sorted[saveIdx++] = arr[rightIdx++];
}
if(leftIdx <= mid) {
for(int i=leftIdx; i<=mid; i++) sorted[saveIdx++] = arr[leftIdx++];
}
else {
for(int i=rightIdx; i<=right; i++) sorted[saveIdx++] = arr[i];
}
for(int i=left; i<=right; i++) arr[i] = sorted[i];
}
}728x90
'Algorithm' 카테고리의 다른 글
| [알고리즘] 퀵 정렬(Quick Sort) - pivot(피벗)을 첫 값으로 잡았을 때 (0) | 2022.04.13 |
|---|---|
| [알고리즘] 퀵 정렬(Quick Sort) - pivot(피벗)을 중앙으로 잡았을 때 (2) | 2022.04.10 |
| [알고리즘] 마스터 정리(도사 정리) (0) | 2022.04.09 |
| [알고리즘] 재귀 함수, 꼬리 재귀 (0) | 2022.04.06 |
| [알고리즘] Brute Force Algorithm(전수 조사 알고리즘) (0) | 2022.04.04 |


댓글