https://www.acmicpc.net/problem/1788
1788번: 피보나치 수의 확장
첫째 줄에 F(n)이 양수이면 1, 0이면 0, 음수이면 -1을 출력한다. 둘째 줄에는 F(n)의 절댓값을 출력한다. 이 수가 충분히 커질 수 있으므로, 절댓값을 1,000,000,000으로 나눈 나머지를 출력한다.
www.acmicpc.net
문제
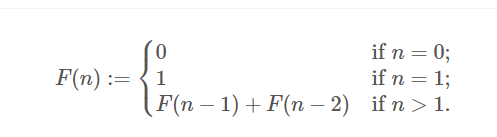
수학에서, 피보나치 수는 위의 점화식과 같이 귀납적으로 정의되는 수열이다. 위의 식에서도 알 수 있듯이, 피보나치 수 F(n)은 0 이상의 n에 대해서만 정의된다.
하지만 피보나치 수 F(n)을 n이 음수인 경우로도 확장시킬 수 있다. 위의 식에서 n > 1인 경우에만 성립하는 F(n) = F(n-1) + F(n-2)를 n ≤ 1일 때도 성립되도록 정의하는 것이다. 예를 들어 n = 1일 때 F(1) = F(0) + F(-1)이 성립되어야 하므로, F(-1)은 1이 되어야 한다.
n이 주어졌을 때, 피보나치 수 F(n)을 구하는 프로그램을 작성하시오. n은 음수로 주어질 수도 있다.
입력
첫째 줄에 n이 주어진다. n은 절댓값이 1,000,000을 넘지 않는 정수이다.
출력
첫째 줄에 F(n)이 양수이면 1, 0이면 0, 음수이면 -1을 출력한다. 둘째 줄에는 F(n)의 절댓값을 출력한다. 이 수가 충분히 커질 수 있으므로, 절댓값을 1,000,000,000으로 나눈 나머지를 출력한다.
해설
피보나치에서 음수까지 고려를 해야하는 문제이다.
문제에도 있듯이 F(1) = F(0) + F(-1)이 성립되어야 하여 F(-1) = 1이 된다.
음수인 몇 가지 경우를 더 살펴보자.F(0) = F(-1) + F(-2)이므로 F(-2) = -1이다.F(-1) = F(-2) + F(-3)이므로 F(-3) = 2이다.F(-2) = F(-3) + F(-4)이므로 F(-4) = -3이 된다.
이쯤에서 양수의 피보나치 값들을 보자.F(2) = 1F(3) = 2F(4) = 3이다.
n이 음수일 때 절대값이 짝수라면 dp[n] = -dp[-n]이고, 홀수라면 dp[n] = dp[-n]이다.
이처럼 dp를 통해 값들을 구해놓은 후 조건에 따라 출력을 해주면 된다.
소스 코드
fun main() = with(System.`in`.bufferedReader()) {
var n = readLine().toInt()
val dp = IntArray(1000001)
dp[0] = 0
dp[1] = 1
for(i in 2 .. 1000000) dp[i] = dp[i-2] % 1000000000 + dp[i-1] % 1000000000
if(n < 0) {
n = -n
if(n % 2 == 0) println("-1\n${dp[n] % 1000000000}")
else println("1\n${dp[n] % 1000000000}")
}
else if(n > 0) println("1\n${dp[n] % 1000000000}")
else println("0\n0")
}'PS(Problem Solving) > BOJ' 카테고리의 다른 글
| [백준/BOJ] 6603번: 로또 (0) | 2022.03.27 |
|---|---|
| [백준/BOJ] 1912번: 연속합 (0) | 2022.03.26 |
| [백준/BOJ] 12847번: 꿀 아르바이트 (0) | 2022.03.06 |
| [백준/BOJ] 3758번: KCPC (0) | 2022.03.06 |
| [백준/BOJ] 13251번: 조약돌 꺼내기 (0) | 2022.03.03 |


댓글