문제
https://www.acmicpc.net/problem/1185
1185번: 유럽여행
첫 줄에는 방문할 나라의 수 N(5 ≤ N ≤ 10,000)과 이 나라들 사이를 연결하는 길의 수 P(N-1 ≤ P ≤ 100,000)가 주어진다. 두 번째 줄에는 N+1번째 줄까지 i+1번째 줄에는 i번째 나라를 방문할 때 드는 비
www.acmicpc.net
해설
- N-1개의 길만을 남겨야 한다.
- 모든 도시를 최소 한번 이상 방문하면서 최소 비용이 드는 방법을 찾고 있다.
- 첫 시작 나라는 민식이가 정할 수 있고, 마지막 나라는 시작 나라이어야 한다.
위 3 문장은 문제에서 가장 핵심이 된다 생각한 것들이다.
우선 1, 2번을 보면 최소 신장 트리를 구해야 한다는 것을 알 수 있다.
이때, 문제에서는 각 나라에 방문하는 비용과 각 나라를 연결하는 도로를 지날 때 필요한 비용이 주어진다.
문제의 예시를 그림과 함께 보자.
이는 임의로 만든 것이다.

이제 위에서 봤던 3번을 보자. 시작 나라와 마지막 나라는 같아야 한다.
즉, 최소 신장 트리를 구하면 각각의 모든 나라를 방문하는 경우의 수를 찾을 수 있다.
다시 시작한 나라로 돌아와야하므로 이때 최소 비용으로 돌아오는 방법은 최소 신장 트리를 그대로 돌아오는 것이다.
즉, 각 나라와 도로를 이동하는데 필요한 비용은 출발 도시의 비용 + 도착 도시의 비용 + 도로 이용 비용 * 2이 된다.

이제 여기서 최소신장 트리를 구하면 시작 나라와 마지막 나라가 같은 경로이며 이때의 최소 비용을 구할 수 있다.
최소 신장 트리를 구하기 위해서는 크루스칼 알고리즘을 사용하면 된다.
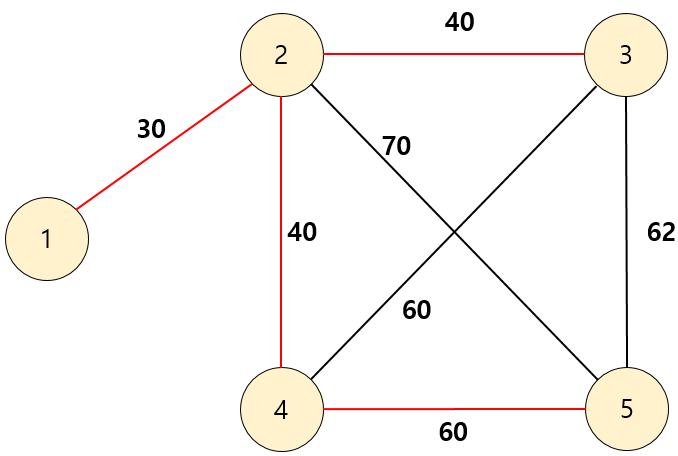
마지막 나라에 도착했을 때도 비용을 지불해야 하는데, 이때 가장 적은 비용이 필요한 나라를 시작 지점으로 잡아야 최소 비용이 될 수 있기에 이 문제에서는 가장 적은 비용이었던 6인 4번 나라가 시작 나라와 도착 나라가 되며, 이 비용을 구했던 최소 비용에 더해주면 된다. 즉 176이 최소 비용이 된다.
코드
import java.util.*
import kotlin.collections.ArrayList
import kotlin.math.min
private lateinit var visitedCost: IntArray
private lateinit var parent: IntArray
data class Info(val from: Int, val to: Int, val cost: Int): Comparable<Info> {
override fun compareTo(other: Info): Int = cost - other.cost
}
fun main() = with(System.`in`.bufferedReader()) {
val (countryCnt, roadCnt) = readLine().split(" ").map { it.toInt() }
visitedCost = IntArray(countryCnt + 1)
parent = IntArray(countryCnt + 1) { i -> i }
var minCost = Integer.MAX_VALUE
repeat(countryCnt) { i ->
visitedCost[i + 1] = readLine().toInt()
minCost = min(minCost, visitedCost[i+1])
}
val pq = PriorityQueue<Info>()
repeat(roadCnt) {
val (from, to, cost) = readLine().split(" ").map { it.toInt() }
pq.add(Info(from, to, visitedCost[from] + visitedCost[to] + 2 * cost))
}
var ans = 0
while(pq.isNotEmpty()) {
val cur = pq.poll()
if(find(cur.from) != find(cur.to)) {
union(cur.from, cur.to)
ans += cur.cost
}
}
println(ans + minCost)
}
private fun union(a: Int, b: Int) {
val aRoot = find(a)
val bRoot = find(b)
if(aRoot < bRoot) parent[bRoot] = aRoot
else parent[aRoot] = bRoot
}
private fun find(node: Int): Int {
if(parent[node] != node) parent[node] = find(parent[node])
return parent[node]
}'PS(Problem Solving) > BOJ' 카테고리의 다른 글
| [백준/BOJ] 16197번: 두 동전 (0) | 2022.09.02 |
|---|---|
| [백준/BOJ] 1719번: 택배 (0) | 2022.09.01 |
| [백준/BOJ] 1613번: 역사 (0) | 2022.08.30 |
| [백준/BOJ] 14938번: 서강그라운드 (1) | 2022.08.29 |
| [백준/BOJ] 16928번: 뱀과 사다리 게임 (0) | 2022.08.28 |


댓글